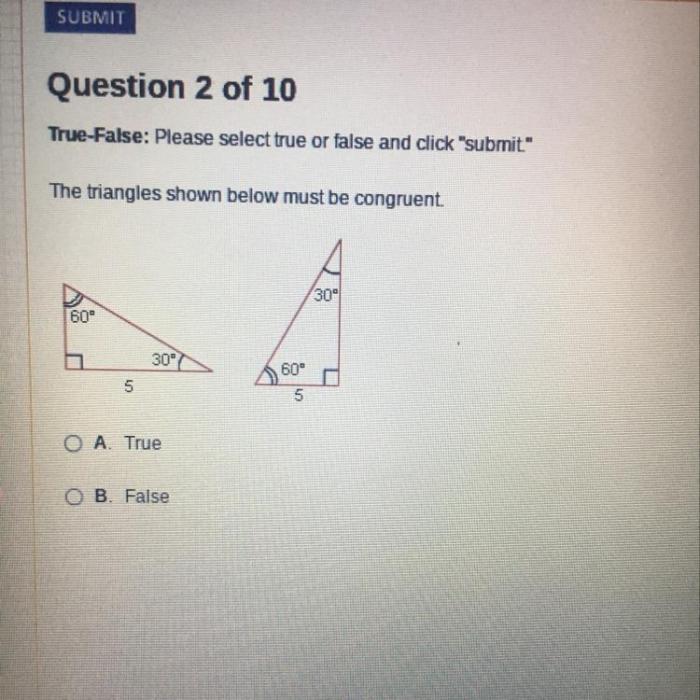
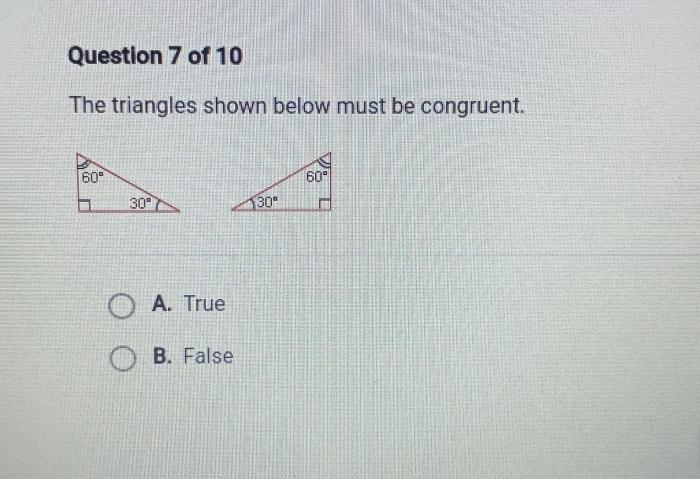
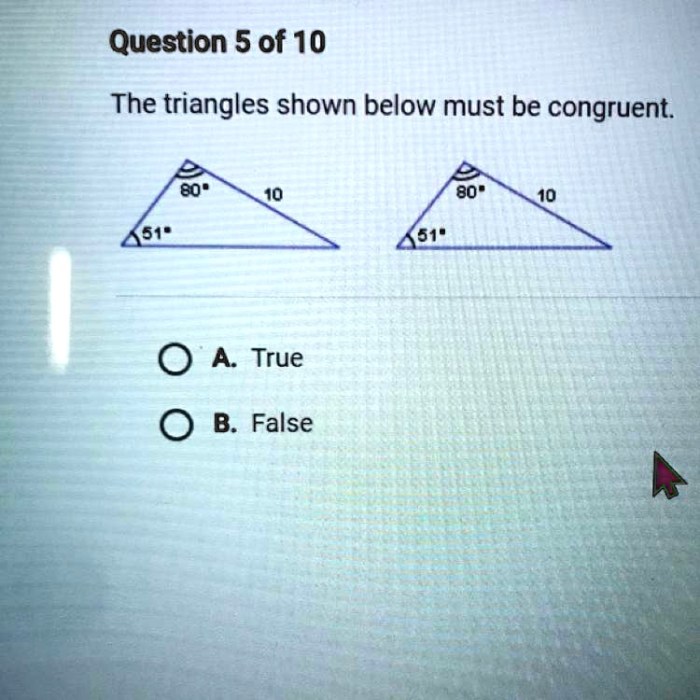
The triangles shown below must be congruent. – The concept of congruent triangles is a fundamental pillar of geometry, providing a solid foundation for understanding the relationships between shapes and their properties. In this comprehensive analysis, we will delve into the intricacies of congruent triangles, examining their definition, methods of identification, properties, and practical applications.
Congruent triangles are geometric figures that share identical corresponding sides and angles. This inherent equality grants them unique characteristics and opens up a wide range of applications across various disciplines, making their study essential for a deeper comprehension of geometry.
1. Definition of Congruent Triangles
In geometry, congruence refers to the equality of shapes and sizes. Congruent triangles are triangles that have the same shape and size. This means that their corresponding sides and angles are equal.
2. Identifying Congruent Triangles
SSS (Side-Side-Side) Congruence Theorem
If the three sides of one triangle are equal to the three sides of another triangle, then the triangles are congruent.
SAS (Side-Angle-Side) Congruence Theorem
If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
ASA (Angle-Side-Angle) Congruence Theorem
If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
AAS (Angle-Angle-Side) Congruence Theorem, The triangles shown below must be congruent.
If two angles and a non-included side of one triangle are equal to two angles and the corresponding side of another triangle, then the triangles are congruent.
3. Properties of Congruent Triangles
Congruent triangles have the following properties:
- Corresponding angles are equal.
- Corresponding sides are equal.
- Corresponding medians are equal.
- Corresponding altitudes are equal.
- Corresponding circumcircles are equal.
- Corresponding inscribed circles are equal.
4. Applications of Congruence
Congruence is used in a variety of applications, including:
- Architecture: To ensure that buildings are symmetrical and balanced.
- Engineering: To design structures that are strong and stable.
- Design: To create aesthetically pleasing objects and environments.
5. Visual Representation of Congruent Triangles: The Triangles Shown Below Must Be Congruent.

| Triangle 1 | Triangle 2 |
|---|---|
 |
 |
| Corresponding Angles | Corresponding Sides |
| ∠A = ∠A’ | AB = A’B’ |
| ∠B = ∠B’ | BC = B’C’ |
| ∠C = ∠C’ | AC = A’C’ |
Questions and Answers
What is the definition of congruent triangles?
Congruent triangles are triangles that have the same corresponding sides and angles.
How can we identify congruent triangles?
Congruent triangles can be identified using congruence theorems such as SSS, SAS, ASA, and AAS.
What are the properties of congruent triangles?
Congruent triangles have corresponding sides and angles that are equal.
Where are congruent triangles used in real-world applications?
Congruent triangles are used in architecture, engineering, and design to ensure accuracy and precision in measurements and constructions.